Building Fraction Concepts Around the Circle
- By Matt Christiansen
- Jan 11, 2018
When I was teaching in the high school, we taught a unit on rational expressions and equations. In simple terms a rational expression is a fraction that has numbers and variables in the numerator, denominator, or both. Because rational expressions behave a lot like fractions, I usually started this unit with a day or two of review of fractions to help students build confidence with this foundational concept. Every year, I was surprised how many students struggled with fraction concepts, and it was clear to me that we needed to do more to build their conceptual understanding in the early grades.
Generally, we are doing better with this, using more and different models to help students really understand the relationships between the part and the whole and also between fractions. Number lines help build conceptual understanding of fraction relationships and area models are useful tools for both relationships and operations. Another tool that helps students build an understanding of both fraction relationships and operations are interlocking fraction circles. The short video below explains how these circles support students’ understanding of fractions.
Fraction circles provide a quick visual representation of fractions, allowing students to explore unit fractions, part-while relationships, order fractions, and add and subtract fractions with and without like denominators. Here are a few ideas for using this visual tool to help students build their conceptual understanding of fractions.
Representing a Fraction with Unit Fractions
The fraction circles make it easy for students to see unit fractions and how larger fractions are composed of unit fractions. Consider the unit fraction 1/5. Use the 1/5 circle to count by 1/5, noting each time that the fraction is made up of the smaller unit fraction. For example, 3/5 is 1/5 + 1/5 + 1/5.

Comparing and Ordering Fractions
Fraction circles provide a visual model that helps students compare and order fractions. Ask students if 4/8 or 4/6 is larger – many students will say 4/8 because 8 is greater than 6. Then have them model both fractions using the fraction circles and check their answer. Have students explain why 4/6 is larger.

These comparison skills help student order fractions from least to greatest or greatest to least. Have students use the fraction circles to put the fractions 6/8, 4/6, and 7/10 in order from least to greatest. Encourage them to justify their solution.
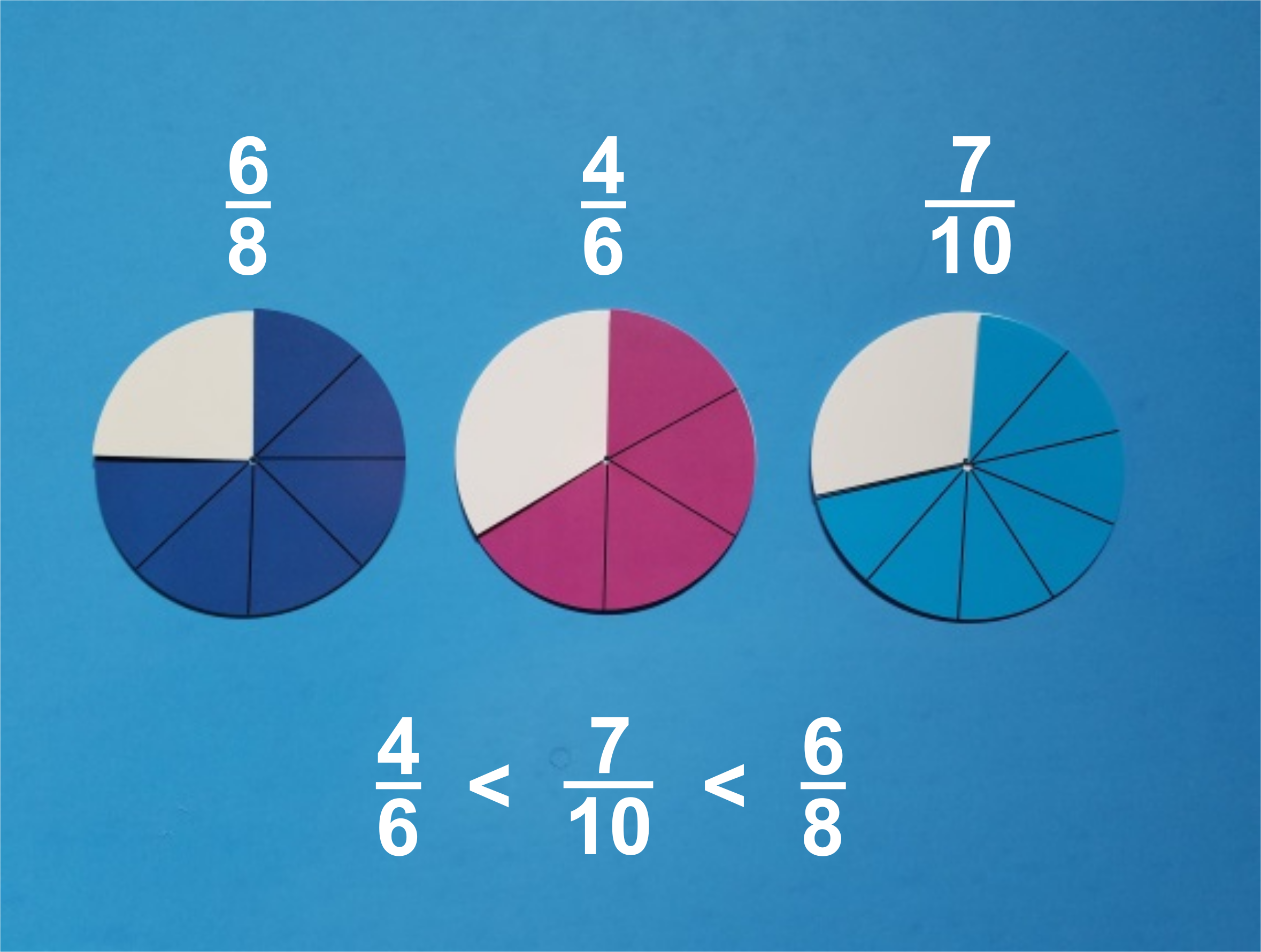
Adding Fractions with Unlike Denominators
When students are first learning to add fractions with unlike denominators, fraction circles provide a visual model for finding a common denominator. For example, ask students to add the fractions 3/4 and 1/6. They will quickly find it difficult to put the fractions together. Ask them to use the fraction circles to find an equivalent fraction for 3/4; they will quickly find 6/8, but may need some help to find 9/12. Now have them find an equivalent fraction for 1/6 – they should find 2/12. Using their equivalent fractions, students should now be able to find the sum, 11/12.
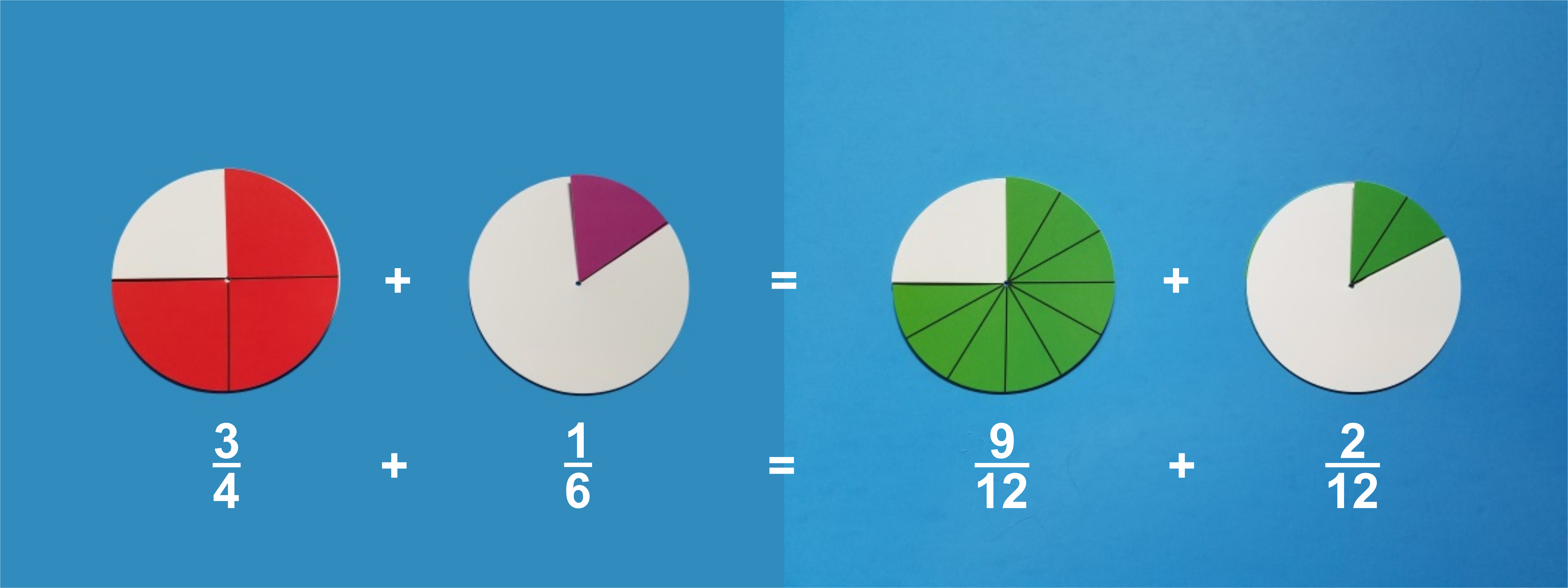
Using fraction circles can help students build a conceptual understanding of fraction relationships and operations that will last long after their initial experience.








 © 2023 Didax, Inc. All Rights Reserved.
© 2023 Didax, Inc. All Rights Reserved.